I've always had the notion that saving money is important and we need to reserve a percentage of our income to achieve a future goal; is a trip, a new car, an apartment or retirement.
That's the financial position I adopt in all my buying decisions and has left me well away from bad debts (explicarei on “Bad Debt” in another post). However, something that never stop to think calmly is the relationship that money has over time.
Everyone agrees that, if a friend borrowed R $ 1,000.00 today and ensure that you return the same R $ 1,000.00 in a year, you will be with a flea in his ear thinking that after these thousand reais one year will not be worth the same amount.
This feeling that the money spent does not buy the same product at present and that today's money will not buy the same product in the future is directly linked to the subject of this post: value of money over time.
The purchasing power of money suffers inflation influences, the exchange rate and interest, and this fluctuation may decrease the power of money. The opposite is also true, in other words, the purchasing power of your money today may increase in the future, since you invest correctly.
In Financial Mathematics discipline my MBA in Business Management from FGV, taught by excellent teacher Fernando Mendonca da Fonseca, this concept was stoned and felt excited to share with you these teachings. The post was a little big but I'm sure that will help you look after your money smarter. Good reading!
 Money Inflation in Time
Money Inflation in Time
As I explained above, the purchasing power of money is influenced by inflation. It erodes this purchasing power over time, in other words, you can no longer buy the same product in the future with the same amount of money it has today. Unless inflation is negative but that I have never seen in Brazil.
When inflation is high perceive this influence quickly, because clearly we note the increase in the price of the product. This increase, for our scope, can be regarded as a direct reflection of inflation.
One example:
Today you want to buy a smartphone that costs R $ 1,000.00, but decided to save that money under the mattress to buy it only when your current cell stops working. After 12 months your cell breaks, you take the money under the mattress, going to the store and now you see the same smartphone costs R $ 1,090.00. This was because the annual inflation was 9% and the product price was reset.
As he kept the money under the mattress, he was not appreciated and lost purchasing power, in other words, you can no longer buy the product with the value it had the 12 months ago.
OBS: In this example I disregarded the depreciation of the asset over time and the reduction in the prices of models from previous versions because of fever of annual launches of new models of this type of product. The example is to focus on the issue of the buying power of your money.
Money on Interest Time
The opposite of purchasing power loss is increasing this power. Still thinking about the example above smarthone, is, instead of having saved money under the mattress, you had invested somewhere that accompany inflation, you would have the same R $ 1,090.00 at the end of 12 months and, therefore, could buy the desired cell, since yields compensate for the loss caused by inflation.
Now imagine if you could invest that money into something that would overcome the losses caused by inflation!? To achieve this you will increase the purchasing power of your money.
Suppose you have invested in a fund that earned 1% per month during these 12 months. At the end of the period those R $ 1,000.00 became R $ 1,126.83.
As now the smartphone costs R $ 1,090.00, you can buy it in cash and still have R $ 36.83 in change to buy a legal hood. You without considering that usually paying in cash you can still negotiate a discount on.
What would you like to fix in your mind here is that there are several investment options in the market that guarantee a return above inflation, in other words, you will be able to easily increase the purchasing power of your hard earned money by investing in the right places. It is not the focus of this post indicate how to do this, or mais important because no time will be explained further.
Pay cash or installments, what the best option?
Many people respond immediately to pay in cash is always the best option, but I say that the correct answer is: non semper.
Why nem semper? Because it will depend on the money in time.
Go straight to the example below will help answer that question and containing a marketing trick that many do not violate.
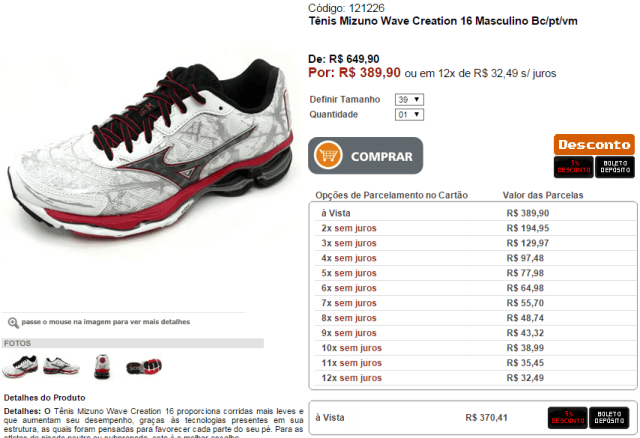
I decided to buy a running shoe and looked pretty on the Internet. The best product for me was the Mizuno Wave Creation 16. A figure offer is na:
The key question I ask is: which the price of tennis?
You'll probably say that the regular price of it is R $ 649.90, but it is selling for R $ 389.90 or incredible 12x R $ 32.49 without interest. If we multiply these shares then we have R $ 389.88, which is two cents cheaper than the price with discount!
This phenomenal promotion, some?
Also found and so I bought tennis, but you missed completely was believed that the product price is R $ 649.90 and R $ 389.90. The real price of shoes is the amount it paid in cash, in other words, R$370,41 (see below in Figure). Therefore, all installments and interest calculations should be based on that value. I explain below.
The Interest inlaid in interest-free installments
How we should always consider the cash value to calculate interest, he is the amount financed, We found that this store is charging 0,80% monthly interest if consumers opt for the installment purchase in 12 times.
The calculation to find out the interest rate in this case is quite simple to be done on a financial calculator, but not the scope of this post. What must be clear is that you will pay R $ 389.90 at the end of 12 months for a product that costs R $ 370.41 today. This difference of R $ 19.49 (R$389,90 – R$370,41) is the amount of interest charged for such funding.
This tennis event the cash payment would be more appropriate, so you do not pay the interest embedded in finance. But there are cases where it is better to pay interest.
When it is better to pay in installments?
Still based in the tennis example, Suppose that the store did not give any discount for cash payment and the lowest value of the product is the same R $ 389.90. In this particular case the installment of interest would be 0%, in other words, interest-free.
The biggest advantage in this case would then divide the purchase in 12 times, because it could invest the product value, rescue the values for the payment of installments, at the end, money would be left for you. See the table below the evolution of this income assuming an investment 1% monthly.
| Period | Invested money | Interest rate | Yield | Benefits |
| 0 | R$ 389,90 | 1% a. m. | R$ 3,90 | R$0,00 |
| 1 | R$ 393,80 | 1% a. m. | R$ 3,94 | R$ 32,49 |
| 2 | R$ 365,25 | 1% a. m. | R$ 3,65 | R$ 32,49 |
| 3 | R$ 336,41 | 1% a. m. | R$ 3,36 | R$ 32,49 |
| 4 | R$ 307,28 | 1% a. m. | R$ 3,07 | R$ 32,49 |
| 5 | R$ 277,87 | 1% a. m. | R$ 2,78 | R$ 32,49 |
| 6 | R$ 248,16 | 1% a. m. | R$ 2,48 | R$ 32,49 |
| 7 | R$ 218,15 | 1% a. m. | R$ 2,18 | R$ 32,49 |
| 8 | R$ 187,84 | 1% a. m. | R$ 1,88 | R$ 32,49 |
| 9 | R$ 157,23 | 1% a. m. | R$ 1,57 | R$ 32,49 |
| 10 | R$ 126,31 | 1% a. m. | R$ 1,26 | R$ 32,49 |
| 11 | R$ 95,08 | 1% a. m. | R$ 0,95 | R$ 32,49 |
| 12 | R$ 63,54 | 1% a. m. | R$ 0,64 | R$ 32,49 |
| 13 | R$ 31,69 | 1% a. m. |
Quickly explaining the concept of this income flow sheet, in zero time you invest the money, which is updated with your income in the next period. The period 1 you get to pay benefits and the money is decreasing, because the provision is greater than income. This account continues until the end of benefits.
After you settle them still have a balance of R $ 31.69 in income from account. This value seems little, but is 8,73% of your initial investment. If the scenario were buying a car of R $ 70,000.00, 8,73% would then be R $ 6,111.00. It's a good deal or not?
Conclusion
I hope this concept of money over time has become very clear in your head and you use that knowledge when analyzing their next purchases.
Always think about your investments are yielding in percentage terms to decide whether it is worthwhile to pay cash or buy in installments. Ideally learn how to perform these calculations but that is for other posts, who knows…
If still remained in some doubt, write a comment for me below I will try to respond as clearly as possible.










Very good !!
Very good, the guy is beast !