Sempre tive a noção de que juntar dinheiro é importante e que precisamos reservar um percentual da nossa renda para alcançar um objetivo futuro; seja uma viagem, um carro novo, um apartamento ou a aposentadoria.
Essa é a postura financeira que adoto em todas as minhas decisões de compra e tem me deixado bem longe das dívidas ruins (explicarei sobre “dívida ruim” em outro post). Porém, uma coisa que nunca paramos para pensar com calma é a relação que o dinheiro tem com o tempo.
Todos concordam que, se um amigo pedir emprestado R$1.000,00 hoje e garantir que te devolverá os mesmos R$1.000,00 daqui a um ano, você ficará com uma pulga atrás da orelha pensando que daqui a um ano esses mil reais não valerão a mesma quantia.
Esse sentimento de que o dinheiro do passado não compra o mesmo produto no presente e que o dinheiro de hoje não comprará o mesmo produto no futuro está diretamente ligado ao assunto desse post: valor do dinheiro no tempo.
O poder de compra do dinheiro sofre influências da inflação, da variação cambial e dos juros, e essa flutuação pode diminuir o poder do dinheiro. O contrário também é verdadeiro, ou seja, o poder de compra do seu dinheiro hoje pode aumentar no futuro, desde que você invista corretamente.
Na disciplina de Matemática Financeira do meu MBA em Gestão Empresarial na FGV, ministrada pelo excelente professor Fernando Mendonça da Fonseca, esse conceito foi lapidado e me senti animado em compartilhar com você esses ensinamentos. O post ficou um pouco grande mas tenho certeza que o ajudará a cuidar do seu dinheiro com mais inteligência. Boa leitura!
 O Dinheiro no Tempo da Inflação
O Dinheiro no Tempo da Inflação
Como expliquei acima, o poder de compra do dinheiro sofre influência da inflação. Ela corrói esse poder de compra com o passar do tempo, ou seja, você não consegue mais comprar o mesmo produto no futuro com o mesmo montante de dinheiro que tem hoje. A não ser que a inflação seja negativa mas isso eu nunca vi no Brasil.
Quando a inflação é muito alta percebemos rapidamente essa influência, pois notamos claramente o aumento no preço do produto. Esse aumento, para o nosso escopo, pode ser considerado como o reflexo direto da inflação.
Vamos a um exemplo:
Hoje você quer comprar um smartphone que custa R$1.000,00, mas decide guardar esse dinheiro embaixo do colchão para comprá-lo somente quando o seu celular atual parar de funcionar. Depois de 12 meses o seu celular quebra, você tira o dinheiro debaixo do colchão, vai até a loja e vê que agora o mesmo smartphone custa R$1.090,00. Isso aconteceu porque a inflação anual foi de 9% e o preço do produto foi reajustado.
Como você manteve o dinheiro debaixo do colchão, ele não se valorizou e perdeu o poder de compra, ou seja, você não consegue mais comprar o produto com o valor que ele tinha a 12 meses atrás.
OBS: Nesse exemplo desconsiderei a depreciação do bem ao longo do tempo e a redução nos preços dos modelos de versões anteriores devido a febre de lançamentos anuais dos novos modelos desse tipo de produto. O exemplo é pra focar na questão do poder de compra do seu dinheiro.
O Dinheiro no Tempo dos Juros
O contrário da perda do poder de compra é o aumento desse poder. Ainda pensando no exemplo do smarthone acima, se, ao invés de ter guardado o dinheiro embaixo do colchão, você o tivesse investido em algum lugar que acompanhasse a inflação, você teria os mesmos R$1.090,00 ao final dos 12 meses e, portanto, conseguiria comprar o celular desejado, pois o rendimento compensaria a perda provocada pela inflação.
Agora imagine se você conseguisse investir esse dinheiro em algo que superasse as perdas provocadas pela inflação!? Se conseguir isso você estará aumentando o poder de compra do seu dinheiro.
Suponha que você tenha investido num fundo que rendeu 1% ao mês durante esses 12 meses. No final do período aqueles R$1.000,00 se transformaram em R$1.126,83.
Como agora o smartphone custa R$1.090,00, você consegue comprá-lo à vista e ainda terá R$36,83 de troco pra comprar uma capinha legal. Isso sem considerar que geralmente pagando à vista você ainda pode negociar um desconto no valor.
O que gostaria de fixar na sua mente até aqui é que existem várias opções de investimento no mercado que garantem um retorno acima da inflação, ou seja, você conseguirá facilmente aumentar o poder de compra do seu suado dinheiro investindo nos lugares certos. Não é o foco desse post indicar como fazer isso, porque o mais importante no momento será explicado a seguir.
Pagar à vista ou parcelado, qual a melhor opção?
Muitas pessoas responderão imediatamente que pagar à vista é sempre a melhor opção, mas digo que a resposta correta é: nem sempre.
Por que nem sempre? Porque vai depender do dinheiro no tempo.
Vamos diretamente ao exemplo abaixo que ajudará a responder a essa pergunta e que contém uma pegadinha de marketing que muitos não se atentam.
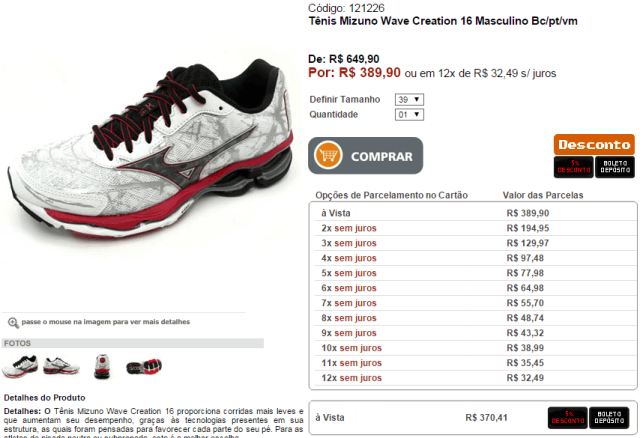
Decidi comprar um tênis de corrida e procurei bastante na internet. O melhor produto para mim foi o Mizuno Wave Creation 16. A oferta está na figura:
A pergunta chave que faço é: qual o preço desse tênis?
Você provavelmente vai dizer que o preço normal dele é R$649,90, mas está sendo vendido por R$389,90 ou incríveis 12x de R$32,49 sem juros. Se multiplicarmos essas parcelas teremos então R$389,88, que é dois centavos mais barato que o preço com o desconto!
Fenomenal essa promoção, certo?
Também achei e por isso comprei o tênis, mas você errou completamente se acreditou que o preço do produto é R$649,90 ou R$389,90. O preço real desse tênis é o valor dele pago à vista, ou seja, R$370,41 (veja mais abaixo na figura). Portanto, todos os cálculos de parcelamento e juros devem ser baseados nesse valor. Explico abaixo.
Os Juros embutidos no parcelamento sem juros
Como devemos sempre considerar o valor à vista para calcularmos os juros, que é ele o valor financiado, constatamos que esta loja está cobrando 0,80% ao mês de juros se o consumidor optar pela compra parcelada em 12 vezes.
O cálculo para descobrir a taxa de juros nesse caso é bem simples de ser feito numa calculadora financeira, mas não é o escopo desse post. O que precisa ficar claro é que você pagará R$389,90 ao final de 12 meses por um produto que custa R$370,41 hoje. Essa diferença de R$19,49 (R$389,90 – R$370,41) é o montante dos juros cobrado por esse financiamento.
Neste caso do tênis o pagamento à vista seria mais indicado, para que você não pague os juros embutidos no financiamento. Mas existem casos em que é melhor pagar os juros.
Quando é melhor pagar parcelado?
Ainda com base no exemplo do tênis, suponhamos que a loja não desse qualquer desconto para o pagamento à vista e que o menor valor do produto seja mesmo os R$389,90. Nesse caso específico os juros do parcelamento seria de 0%, ou seja, sem juros.
A maior vantagem neste caso seria então parcelar a compra em 12 vezes, pois você poderia investir o valor do produto, resgatar os valores para o pagamento das parcelas e, no fim, sobraria dinheiro pra você. Veja na tabela abaixo a evolução desse rendimento supondo um investimento de 1% ao mês.
| Período | Dinheiro Investido | Taxa de Juros | Rendimento | Prestações |
| 0 | R$ 389,90 | 1% a. m. | R$ 3,90 | R$0,00 |
| 1 | R$ 393,80 | 1% a. m. | R$ 3,94 | R$ 32,49 |
| 2 | R$ 365,25 | 1% a. m. | R$ 3,65 | R$ 32,49 |
| 3 | R$ 336,41 | 1% a. m. | R$ 3,36 | R$ 32,49 |
| 4 | R$ 307,28 | 1% a. m. | R$ 3,07 | R$ 32,49 |
| 5 | R$ 277,87 | 1% a. m. | R$ 2,78 | R$ 32,49 |
| 6 | R$ 248,16 | 1% a. m. | R$ 2,48 | R$ 32,49 |
| 7 | R$ 218,15 | 1% a. m. | R$ 2,18 | R$ 32,49 |
| 8 | R$ 187,84 | 1% a. m. | R$ 1,88 | R$ 32,49 |
| 9 | R$ 157,23 | 1% a. m. | R$ 1,57 | R$ 32,49 |
| 10 | R$ 126,31 | 1% a. m. | R$ 1,26 | R$ 32,49 |
| 11 | R$ 95,08 | 1% a. m. | R$ 0,95 | R$ 32,49 |
| 12 | R$ 63,54 | 1% a. m. | R$ 0,64 | R$ 32,49 |
| 13 | R$ 31,69 | 1% a. m. |
Explicando rapidamente o conceito dessa planilha de fluxo de rendimento, no período zero você investe o dinheiro, que é atualizado com seu rendimento no período seguinte. No período 1 você começa a pagar as prestações e o dinheiro vai diminuindo, pois a prestação é maior que os rendimentos. Essa conta prossegue até o final das prestações.
Após quitá-las ainda tens um saldo de R$31,69 na conta proveniente dos rendimentos. Esse valor parece pouco, mas representa 8,73% do seu investimento inicial. Se o cenário fosse a compra de um carro de R$70.000,00, 8,73% seria então R$6.111,00. É uma boa quantia ou não é?
Conclusão
Espero que esse conceito do dinheiro no tempo tenha ficado bem claro na sua cabeça e que você utilize esse conhecimento quando for analisar as suas próximas compras.
Pense sempre em quanto os seus investimentos estão rendendo em termos percentuais pra decidir se vale a pena pagar à vista ou comprar parcelado. O ideal seria aprender a realizar esses cálculos mas isso fica para outros posts, quem sabe…
Se ainda permaneceu com alguma dúvida, escreva um comentário pra mim logo abaixo que tentarei responder da forma mais clara possível.










Muito bom !!
Muito bom, o cara é fera !